NumPy linspace(): Cum se creează matrice de numere uniform distanțate

Acest tutorial vă va învăța cum să utilizați NumPy linspace() pentru a crea o matrice de numere spațiate uniform în Python.

Veți învăța sintaxa lui NumPy linspace() , urmată de exemple care vă vor ajuta să înțelegeți cum să o utilizați.

Notă: Pentru a urma acest tutorial, trebuie să aveți instalate Python și NumPy.

Nu aveți încă NumPy? Am creat un ghid rapid de instalare pentru tine.

Să începem!

Instalați și importați NumPy

Înainte de a începe tutorialul, să parcurgem rapid pașii de instalare a bibliotecii NumPy.

Dacă aveți deja instalat NumPy, nu ezitați să treceți la secțiunea următoare.

• Dacă utilizați Google Colab, un mediu de notebook Jupyter bazat pe cloud, puteți importa NumPy și puteți începe codarea imediat. (recomandat pentru acest tutorial)
• Dacă doriți să configurați un mediu de lucru local, vă recomand să instalați distribuția Anaconda a Python. Anaconda vine cu mai multe pachete utile preinstalate. Puteți descărca programul de instalare pentru sistemul dvs. de operare. Procesul de configurare durează doar câteva minute.
• Dacă aveți deja instalat Python pe computer, puteți instala în continuare distribuția Anaconda. Puteți folosi conda sau pip pentru a instala și gestiona pachetele. Puteți rula una dintre următoarele comenzi din linia de comandă Anaconda pentru a instala NumPy.

 # Install NumPy using conda conda install numpy # Install NumPy using pip pip install numpy

Ca pas următor, importați numpy sub alias np , rulând următoarea comandă. Acest lucru vă va ajuta să faceți referire la NumPy ca np — fără a fi nevoie să tastați numpy de fiecare dată când accesați un element din modul.

 import numpy as np

În continuare, vom folosi notația cu puncte pentru a accesa toate funcțiile din biblioteca NumPy astfel: np.<func-name> .

Cazul numerelor uniform distanțate

Când lucrați cu matrice NumPy, există momente în care va trebui să creați o matrice de numere spațiate uniform într-un interval.

Înainte de a merge mai departe, să trecem rapid peste o altă funcție similară np.arange() .

NumPy linspace() vs. NumPy arange()

Dacă ați mai folosit NumPy, probabil că ați fi folosit np.arange() pentru a crea o matrice de numere într-un interval specificat.

Știți că np.arange(start, stop, step) returnează o serie de numere de la start până la, dar fără a include stop , în pași de step ; dimensiunea implicită a pasului fiind 1.

Cu toate acestea, valoarea pasului poate să nu fie întotdeauna evidentă. Să vedem de ce este cazul.

De exemplu, dacă aveți nevoie de 4 numere uniform distanțate între 0 și 1, știți că dimensiunea pasului trebuie să fie 0,25. Dar dacă utilizați np.arange() , nu include valoarea stop de 1. Deci va trebui să alegeți un interval care depășește valoarea stop.

Următoarea imagine ilustrează alte câteva exemple în care aveți nevoie de un anumit număr de puncte uniform distanțate în intervalul [a, b].

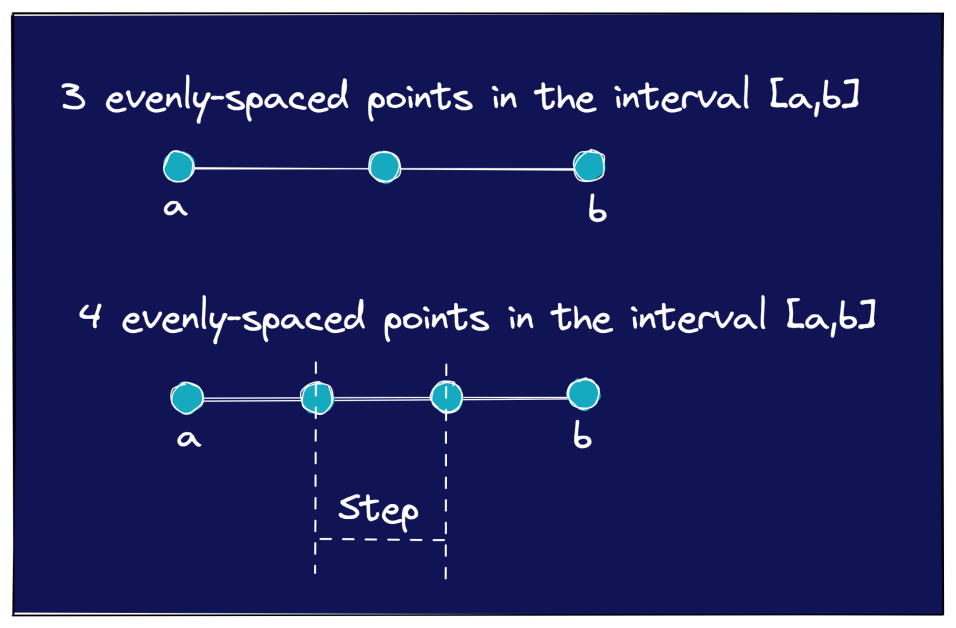
Primul nostru exemplu de 4 puncte uniform distanțate în [0,1] a fost destul de ușor. Știți că dimensiunea pasului dintre puncte ar trebui să fie de 0,25.

Să presupunem că aveți un exemplu puțin mai implicat – în care a trebuit să enumerați 7 puncte uniform distanțate între 1 și 33. Aici, dimensiunea pasului poate să nu fie foarte clară imediat. Puteți, totuși, să calculați manual valoarea step în acest caz.

Cu toate acestea, np.linspace() este aici pentru a vă face și mai simplu!

Când utilizați np.linspace() , trebuie doar să specificați numărul de puncte din interval - fără să vă faceți griji cu privire la dimensiunea pasului. Și veți primi înapoi matricea după cum doriți.

Cu această motivație, să continuăm să învățăm sintaxa lui NumPy linspace() în secțiunea următoare.

Sintaxa lui NumPy linspace()

Sintaxa pentru utilizarea NumPy linspace() este prezentată mai jos:

 np.linspace(start, stop, num, endpoint, retstep, dtype, axis)

La început, sintaxa de mai sus poate părea foarte complicată cu mulți parametri.

Cu toate acestea, majoritatea sunt parametri opționali și vom ajunge la o sintaxă mult mai simplă în doar câteva minute.

Acum să începem prin a analiza sintaxa de mai sus:

• start și stop sunt punctele de început și, respectiv, de sfârșit ale intervalului. Atât start cât și stop pot fi scalari sau matrice. Ne vom limita la valorile scalare de început și de sfârșit în acest tutorial.
• num este numărul de puncte uniform distanțate. Și este un parametru opțional cu o valoare implicită de 50.
• endpoint este, de asemenea, un parametru opțional care poate fi adevărat sau fals.
• Valoarea implicită este True, ceea ce înseamnă că punctul final va fi inclus în interval în mod implicit. Cu toate acestea, îl puteți seta la Fals pentru a exclude punctul final.
• retstep este încă un parametru opțional care ia valorile booleene True sau False. Când este setată la True, valoarea pasului este returnată.
• dtype este tipul de date al numerelor din matrice. Tipul este de obicei dedus ca float și nu trebuie furnizat în mod explicit.
• axis este un alt parametru opțional care indică axa de-a lungul căreia trebuie stocate numerele. Și acest lucru este relevant doar atunci când valorile de start și de stop sunt în sine matrice.

️ Deci, ce np.linspace() ?

Returnează o matrice N-dimensională de numere uniform distanțate. Și dacă parametrul retstep este setat la True , returnează și dimensiunea pasului.

Pe baza discuției de până acum, iată o sintaxă simplificată pentru a utiliza np.linspace() :

 np.linspace(start, stop, num)

Linia de cod de mai sus va returna o matrice de num numere spațiate uniform în intervalul [start, stop] .

Acum că știți sintaxa, să începem să codificăm exemple.

Cum se creează matrice uniform distanțate cu NumPy linspace()

#1. Ca prim exemplu, să creăm o matrice de 20 de numere uniform distanțate în intervalul [1, 5].

Puteți specifica valorile start , stop și num ca argumente ale cuvintelor cheie. Acest lucru este afișat în celula de cod de mai jos:

 import numpy as np arr1 = np.linspace(start = 1,stop = 5,num = 20) print(arr1) # Output: [1. 1.21052632 1.42105263 1.63157895 1.84210526 2.05263158 2.26315789 2.47368421 2.68421053 2.89473684 3.10526316 3.31578947 3.52631579 3.73684211 3.94736842 4.15789474 4.36842105 4.57894737 4.78947368 5. ]

Observați cum numerele din matrice încep la 1 și se termină la 5, inclusiv ambele puncte finale. De asemenea, observați cum numerele, inclusiv punctele 1 și 5, sunt reprezentate ca float în tabloul returnat.

#2. În exemplul anterior, ați trecut valorile pentru start , stop și num ca argumente ale cuvintelor cheie . Dacă introduceți argumentele în ordinea corectă, ați putea la fel de bine să le utilizați ca argumente de poziție doar cu valorile, așa cum se arată mai jos.

 import numpy as np arr2 = np.linspace(1,5,20) print(arr2) # Output: [1. 1.21052632 1.42105263 1.63157895 1.84210526 2.05263158 2.26315789 2.47368421 2.68421053 2.89473684 3.10526316 3.31578947 3.52631579 3.73684211 3.94736842 4.15789474 4.36842105 4.57894737 4.78947368 5. ]

#3. Acum să creăm o altă matrice în care setăm retstep la True .

Aceasta înseamnă că funcția va returna acum atât matricea, cât și pasul. Și le putem despacheta în două variabile arr3 : matricea și step_size : dimensiunea pasului returnat.

Următoarea celulă de cod explică cum puteți face acest lucru.

 import numpy as np arr3, step_size = np.linspace(1,5,20,retstep = True) print(arr3) # Output: [1. 1.21052632 1.42105263 1.63157895 1.84210526 2.05263158 2.26315789 2.47368421 2.68421053 2.89473684 3.10526316 3.31578947 3.52631579 3.73684211 3.94736842 4.15789474 4.36842105 4.57894737 4.78947368 5. ] # Output: print(step_size) 0.21052631578947367

#4. Ca exemplu final, să setăm endpoint la False și să verificăm ce se întâmplă.

 import numpy as np arr4 = np.linspace(1,5,20,endpoint = False) print(arr4) # Output: [1. 1.2 1.4 1.6 1.8 2. 2.2 2.4 2.6 2.8 3. 3.2 3.4 3.6 3.8 4. 4.2 4.4 4.6 4.8]

În tabloul returnat, puteți vedea că 1 este inclus, în timp ce 5 nu este inclus. Și ultima valoare din matrice se întâmplă să fie 4,8, dar mai avem 20 de numere.

Până acum, am generat doar matrice de numere uniform distanțate. În secțiunea următoare, să vizualizăm prin trasarea acestor numere.

Cum se trasează numere uniform distanțate într-un interval

În această secțiune, să alegem [10,15] ca interval de interes. Și apoi, utilizați np.linspace() pentru a genera două tablouri, fiecare cu 8 și, respectiv, 12 puncte.

După ce aceasta este finalizată, putem folosi funcția de trasare din biblioteca matplotlib pentru a le trasa.

Pentru claritate, vom fixa cele două rețele de N1 = 8 și N2 = 12 puncte uniform distanțate în poziții diferite de-a lungul axei y.

Următorul fragment de cod demonstrează acest lucru.

 import numpy as np import matplotlib.pyplot as plt N1 = 8 N2 = 12 a = 10 b = 15 y1 = np.zeros(N1) y2 = np.zeros(N2) x1 = np.linspace(a, b, N1) x2 = np.linspace(a, b, N2) plt.plot(x1, y1-0.5, 'o') plt.plot(x2, y2 + 0.5, 'o') plt.ylim([-1, 1]) plt.title(f'Evenly Spaced Numbers in the Interval [{a},{b}]') plt.xlabel('Interval') plt.show()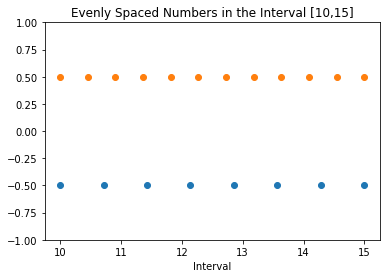

Generarea de puncte uniform distanțate poate fi utilă atunci când lucrați cu funcții matematice. Vom afla despre asta în secțiunea următoare.

Cum să utilizați NumPy linspace() cu funcții matematice

După ce ați generat o matrice de numere uniform distanțate folosind np.linspace() , puteți calcula valorile funcțiilor matematice din interval.

În celula de cod de mai jos, generați mai întâi 50 de puncte uniform distanțate în intervalul de la 0 la 2π. Și apoi creați matricea y folosind np.sin() pe matricea x . Rețineți că puteți sări peste parametrul num , deoarece valoarea implicită este 50. Îl vom folosi în continuare în mod explicit.

Ca un pas următor, puteți reprezenta grafic funcția sinus în intervalul [0, 2π]. Pentru a face acest lucru, puteți utiliza matplotlib, ca în exemplul anterior. În mod specific, funcția plot() din matplotlib.pytplot este utilizată pentru a crea un grafic de linii.

 import numpy as np import matplotlib.pyplot as plt N = 50 a = 0.0 b = 2*np.pi x = np.linspace(a, b, N) y = np.sin(x) plt.plot(x, y, marker = "o") plt.ylim([-1, 1]) plt.title(f'y = sin(x)') plt.xlabel('x ---->') plt.show()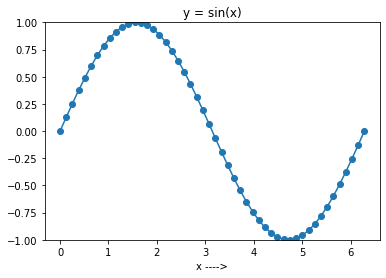

Acum, rulați codul de mai sus setând N egal cu 10. Veți obține graficul așa cum se arată în figura de mai jos.

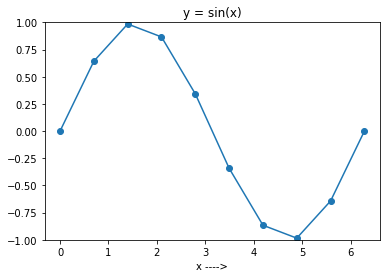
Și puteți vedea că intriga nu este foarte netedă, deoarece ați adunat doar 10 puncte în interval.

În general, cu cât numărul de puncte luate în considerare este mai mare, cu atât graficul funcției va fi mai fin.

Concluzie

Iată un rezumat a ceea ce am învățat.

• np.linspace(start, stop, num) returnează o matrice de num numere spațiate uniform în intervalul [start, stop] .
• Setați punctul final al parametrului opțional la Fals pentru a exclude stop și setați intervalul la [start, stop) .
• Setați opțional retstep la True pentru a obține dimensiunea pasului.
• Generați matrice uniform distanțate folosind np.linspace() și apoi utilizați matricea cu funcții matematice.

Sper că acum înțelegeți cum funcționează np.linspace() . Puteți alege să rulați exemplele de mai sus în blocnotesul Jupyter. Consultați ghidul nostru despre notebook-ul Jupyter sau alte alternative Jupyter pe care le puteți lua în considerare.

Ne vedem cu toții în curând într-un alt tutorial Python. Până atunci, continuați să codificați!