NumPy linspace(): come creare matrici di numeri equidistanti
Pubblicato: 2022-04-11Questo tutorial ti insegnerà come usare NumPy linspace() per creare una matrice di numeri equidistanti in Python.
Imparerai la sintassi di NumPy linspace() , seguita da esempi che ti aiuteranno a capire come usarlo.
Nota: per seguire questo tutorial, devi avere installato Python e NumPy.
Non hai ancora NumPy? Abbiamo messo insieme una guida rapida all'installazione per te.
Iniziamo!
Installa e importa NumPy
Prima di iniziare il tutorial, eseguiamo rapidamente i passaggi per installare la libreria NumPy.
Se hai già installato NumPy, sentiti libero di saltare alla sezione successiva.
- Se utilizzi Google Colab, un ambiente notebook Jupyter basato su cloud, puoi importare NumPy e iniziare subito a scrivere codice. (consigliato per questo tutorial)
- Se desideri configurare un ambiente di lavoro locale, ti consiglio di installare la distribuzione Anaconda di Python. Anaconda viene fornito con diversi pacchetti utili preinstallati. Puoi scaricare il programma di installazione per il tuo sistema operativo. Il processo di installazione richiede solo pochi minuti.
- Se hai già installato Python sul tuo computer, puoi comunque installare la distribuzione Anaconda. Puoi usare conda o pip per installare e gestire i pacchetti. È possibile eseguire uno dei seguenti comandi dal prompt dei comandi di Anaconda per installare NumPy.
# Install NumPy using conda conda install numpy # Install NumPy using pip pip install numpy Come passaggio successivo, importa numpy con l'alias np eseguendo il comando seguente. Ciò ti aiuterà a fare riferimento a NumPy come np , senza dover digitare numpy ogni volta che accedi a un elemento nel modulo.
import numpy as np Andando avanti, useremo la notazione del punto per accedere a tutte le funzioni nella libreria NumPy in questo modo: np.<func-name> .
Il caso di numeri equidistanti
Quando si lavora con gli array NumPy, a volte è necessario creare un array di numeri equidistanti in un intervallo.
Prima di andare oltre, esaminiamo rapidamente un'altra funzione simile np.arange() .
NumPy linspace() vs. NumPy arange()
Se hai usato NumPy prima, probabilmente avresti usato np.arange() per creare una matrice di numeri all'interno di un intervallo specificato.
Sai che
np.arange(start, stop, step)restituisce un array di numeri dastartup astop, escluso, nei passaggi distep; la dimensione del passo predefinita è 1.
Tuttavia, il valore del passo potrebbe non essere sempre evidente. Vediamo perché questo è il caso.
Ad esempio, se hai bisogno di 4 numeri equidistanti tra 0 e 1, sai che la dimensione del passo deve essere 0,25. Ma se stai usando np.arange() , non include il valore di stop di 1. Quindi dovrai scegliere un intervallo che vada oltre il valore di stop.
L'immagine seguente illustra alcuni altri esempi in cui è necessario un numero specifico di punti equidistanti nell'intervallo [a, b].
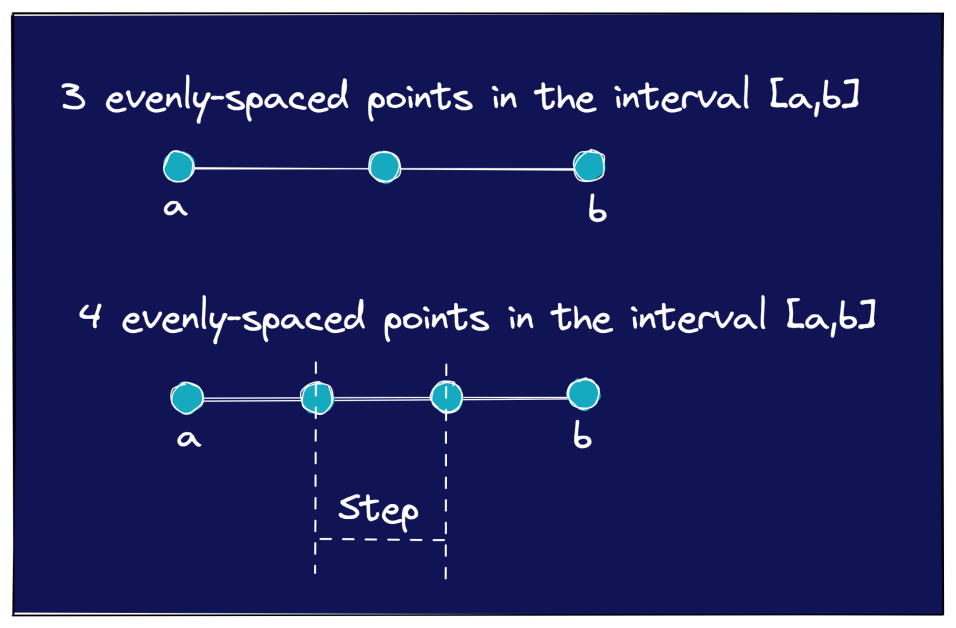
Il nostro primo esempio di 4 punti equidistanti in [0,1] è stato abbastanza facile. Sai che la dimensione del passo tra i punti dovrebbe essere 0,25.
Supponiamo di avere un esempio leggermente più complesso, in cui dovevi elencare 7 punti equidistanti tra 1 e 33. Qui, la dimensione del passo potrebbe non essere molto chiara immediatamente. In questo caso, tuttavia, è possibile calcolare manualmente il valore del step .
Tuttavia, np.linspace() è qui per renderlo ancora più semplice per te!

Quando si utilizza np.linspace() , è sufficiente specificare il numero di punti nell'intervallo, senza preoccuparsi della dimensione del passo. E riavrai l'array come desideri.
Con questa motivazione, procediamo ad imparare la sintassi di NumPy linspace() nella prossima sezione.
Sintassi di NumPy linspace()
La sintassi per l'utilizzo di NumPy linspace() è mostrata di seguito:
np.linspace(start, stop, num, endpoint, retstep, dtype, axis)All'inizio, la sintassi di cui sopra può sembrare molto complicata con molti parametri.
Tuttavia, la maggior parte di essi sono parametri opzionali e arriveremo a una sintassi molto più semplice in un paio di minuti.
Ora iniziamo analizzando la sintassi sopra:
-
startestopsono rispettivamente i punti di inizio e fine dell'intervallo. Sia start che stop possono essere scalari o array. Ci limiteremo ai valori scalari di inizio e fine in questo tutorial. -
numè il numero di punti equidistanti. Ed è un parametro opzionale con un valore predefinito di 50. -
endpointè anche un parametro facoltativo che può essere True o False. - Il valore predefinito è True, il che significa che il punto finale sarà incluso nell'intervallo per impostazione predefinita. Tuttavia, puoi impostarlo su False per escludere il punto finale.
-
retstepè un altro parametro facoltativo che accetta i booleani True o False. Quando è impostato su True, viene restituito il valore del passaggio. -
dtypeè il tipo di dati dei numeri nell'array. Il tipo viene generalmente dedotto come float e non deve essere fornito in modo esplicito. -
axisè un altro parametro opzionale che indica l'asse lungo il quale devono essere memorizzati i numeri. E questo è rilevante solo quando i valori distartestopsono gli stessi array.
️ Quindi cosa np.linspace() ?
Restituisce una matrice N-dimensionale di numeri equidistanti. E se il parametro retstep è impostato su True , restituisce anche la dimensione del passo.
Sulla base della discussione finora, ecco una sintassi semplificata per utilizzare np.linspace() :
np.linspace(start, stop, num)La riga di codice sopra restituirà una matrice di
numnumeri equidistanti nell'intervallo[start, stop].
Ora che conosci la sintassi, iniziamo a codificare esempi.
Come creare array a spaziatura uniforme con NumPy linspace()
# 1. Come primo esempio, creiamo una matrice di 20 numeri equidistanti nell'intervallo [1, 5].

È possibile specificare i valori di start , stop e num come argomenti della parola chiave. Questo è mostrato nella cella del codice qui sotto:
import numpy as np arr1 = np.linspace(start = 1,stop = 5,num = 20) print(arr1) # Output: [1. 1.21052632 1.42105263 1.63157895 1.84210526 2.05263158 2.26315789 2.47368421 2.68421053 2.89473684 3.10526316 3.31578947 3.52631579 3.73684211 3.94736842 4.15789474 4.36842105 4.57894737 4.78947368 5. ] Nota come i numeri nella matrice iniziano con 1 e terminano con 5, inclusi entrambi i punti finali. Inoltre, osserva come i numeri, inclusi i punti 1 e 5, sono rappresentati come float nella matrice restituita.
#2. Nell'esempio precedente, hai passato i valori per start , stop e num come argomenti della parola chiave . Se passi gli argomenti nell'ordine corretto, potresti anche usarli come argomenti posizionali con solo i valori, come mostrato di seguito.
import numpy as np arr2 = np.linspace(1,5,20) print(arr2) # Output: [1. 1.21052632 1.42105263 1.63157895 1.84210526 2.05263158 2.26315789 2.47368421 2.68421053 2.89473684 3.10526316 3.31578947 3.52631579 3.73684211 3.94736842 4.15789474 4.36842105 4.57894737 4.78947368 5. ] #3. Ora creiamo un altro array in cui impostiamo retstep su True .
Ciò significa che la funzione ora restituirà sia l'array che il passaggio. E possiamo decomprimerli in due variabili arr3 : l'array e step_size : la dimensione del passaggio restituita.
La seguente cella di codice spiega come puoi farlo.
import numpy as np arr3, step_size = np.linspace(1,5,20,retstep = True) print(arr3) # Output: [1. 1.21052632 1.42105263 1.63157895 1.84210526 2.05263158 2.26315789 2.47368421 2.68421053 2.89473684 3.10526316 3.31578947 3.52631579 3.73684211 3.94736842 4.15789474 4.36842105 4.57894737 4.78947368 5. ] # Output: print(step_size) 0.21052631578947367 #4. Come ultimo esempio, impostiamo endpoint su False e controlliamo cosa succede.
import numpy as np arr4 = np.linspace(1,5,20,endpoint = False) print(arr4) # Output: [1. 1.2 1.4 1.6 1.8 2. 2.2 2.4 2.6 2.8 3. 3.2 3.4 3.6 3.8 4. 4.2 4.4 4.6 4.8]Nell'array restituito, puoi vedere che 1 è incluso, mentre 5 non è incluso. E l'ultimo valore nell'array sembra essere 4,8, ma abbiamo ancora 20 numeri.
Finora, abbiamo generato solo matrici di numeri equidistanti. Nella prossima sezione, visualizziamo tracciando questi numeri.
Come tracciare numeri a spaziatura uniforme in un intervallo
In questa sezione, scegliamo [10,15] come intervallo di interesse. E poi, usa np.linspace() per generare due array, ciascuno con 8 e 12 punti, rispettivamente.
Al termine, possiamo utilizzare la funzione di tracciamento dalla libreria matplotlib per tracciarli.
Per chiarezza, bloccheremo le due matrici di N1 = 8 e N2 = 12 punti equidistanti in posizioni diverse lungo l'asse y.
Il seguente frammento di codice lo dimostra.
import numpy as np import matplotlib.pyplot as plt N1 = 8 N2 = 12 a = 10 b = 15 y1 = np.zeros(N1) y2 = np.zeros(N2) x1 = np.linspace(a, b, N1) x2 = np.linspace(a, b, N2) plt.plot(x1, y1-0.5, 'o') plt.plot(x2, y2 + 0.5, 'o') plt.ylim([-1, 1]) plt.title(f'Evenly Spaced Numbers in the Interval [{a},{b}]') plt.xlabel('Interval') plt.show() 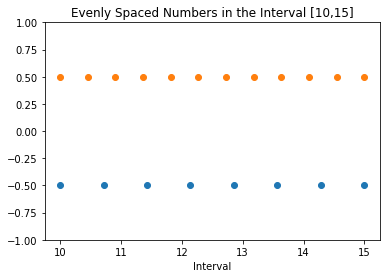
La generazione di punti equidistanti può essere utile quando si lavora con funzioni matematiche. Lo impareremo nella prossima sezione.
Come utilizzare NumPy linspace() con funzioni matematiche
Dopo aver generato una matrice di numeri equidistanti usando np.linspace() , puoi calcolare i valori delle funzioni matematiche nell'intervallo.
Nella cella del codice sottostante, generi prima 50 punti equidistanti nell'intervallo da 0 a 2π. E quindi crea l'array y usando np.sin() sull'array x . Nota che puoi saltare il parametro num , poiché il valore predefinito è 50. Lo useremo comunque in modo esplicito.
Come passaggio successivo, puoi tracciare la funzione seno nell'intervallo [0, 2π]. Per fare ciò, puoi usare matplotlib, come nell'esempio precedente. In particolare, la funzione plot() in matplotlib.pytplot viene utilizzata per creare un grafico a linee.
import numpy as np import matplotlib.pyplot as plt N = 50 a = 0.0 b = 2*np.pi x = np.linspace(a, b, N) y = np.sin(x) plt.plot(x, y, marker = "o") plt.ylim([-1, 1]) plt.title(f'y = sin(x)') plt.xlabel('x ---->') plt.show() 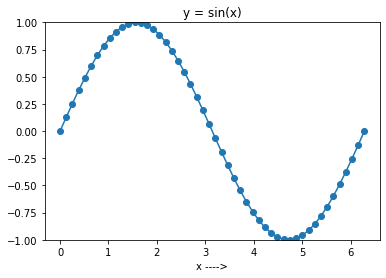
Ora, esegui il codice sopra impostando N uguale a 10. Otterrai il grafico come mostrato nella figura seguente.
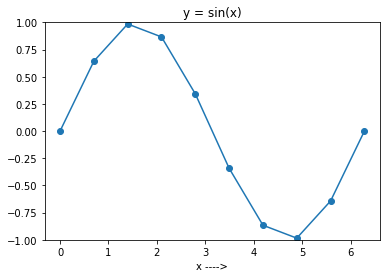
E puoi vedere che la trama non è molto fluida, dato che hai selezionato solo 10 punti nell'intervallo.
In generale, maggiore è il numero di punti che consideri, più liscia sarà la trama della funzione.
Conclusione
Ecco un riassunto di ciò che abbiamo imparato.
- np.linspace(start, stop, num) restituisce una matrice di num numeri equidistanti nell'intervallo [start, stop] .
- Impostare l' endpoint del parametro facoltativo su False per escludere stop e impostare l'intervallo su [start, stop) .
- Impostare retstep su True facoltativamente per ottenere la dimensione del passaggio.
- Genera array a spaziatura uniforme usando np.linspace() , quindi usa l'array con funzioni matematiche.
Spero che ora tu capisca come funziona np.linspace() . Puoi scegliere di eseguire gli esempi precedenti nel notebook Jupyter. Dai un'occhiata alla nostra guida sul notebook Jupyter o su altre alternative Jupyter che puoi prendere in considerazione.
A presto in un altro tutorial Python. Fino ad allora, continua a programmare!
